首先对于如下的多边形：

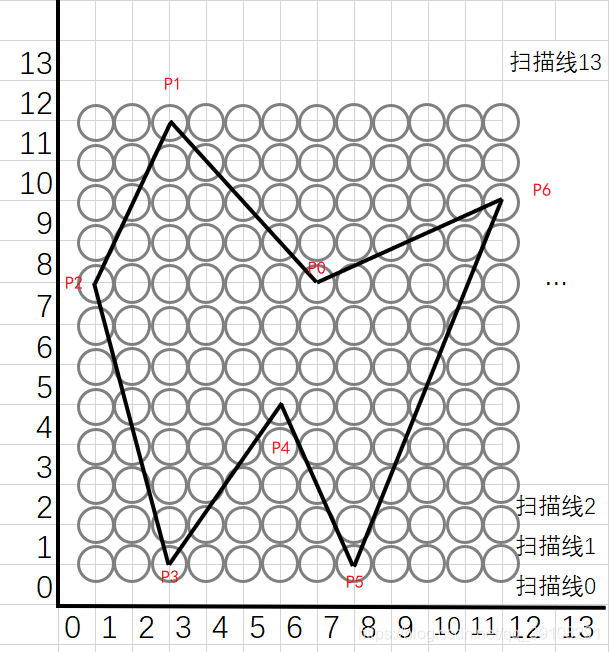
1.有效边表填充算法

1.1.有效边表填充算法分为如下几个步骤：

​ 1.1.1.将多边形所有的边分别与扫描线1计算交点，得到交点集，与扫描线计算的边没有顺序要求。
​ 1.1.2.将点集按标x的大小递增排序，得到有序点集。
​ 1.1.3.将有序点集两两配对，得到对应的像素区间。
​ 1.1.4.将像素区间内的像素填充颜色，至此第一条扫描线上处于多边形内的的像素填充完毕。
​ 1.1.5.扫描线标号加1，重复以上步骤，直至到最后一条扫描线。
​ 如：对于扫描线3（y=3）与多边形所有的边计算交点，得到与P3P4交于点（4.5，3），与P3P2交于点（2.4，3），与P5P6交于点（8.8，3），与P5P4交于点（7，3）。
​ 圆整处理得到点集（5，3）、（2，3）、（9，3）、（7，3）。
​ 递增排序得到有序点集（2，3）、（5，3）、（7，3）、（9，3）。
​ 两两配对得到扫描线3上的填充像素区间[2，5]、[7，9]。
​ 填充区间内的所有像素。
​ 得到如图所示的填充效果：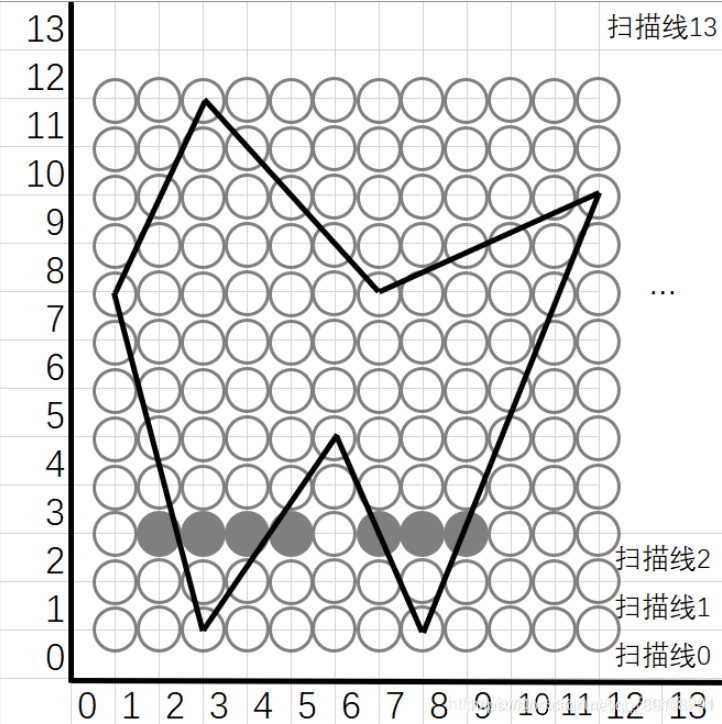

全部填充得到如下效果：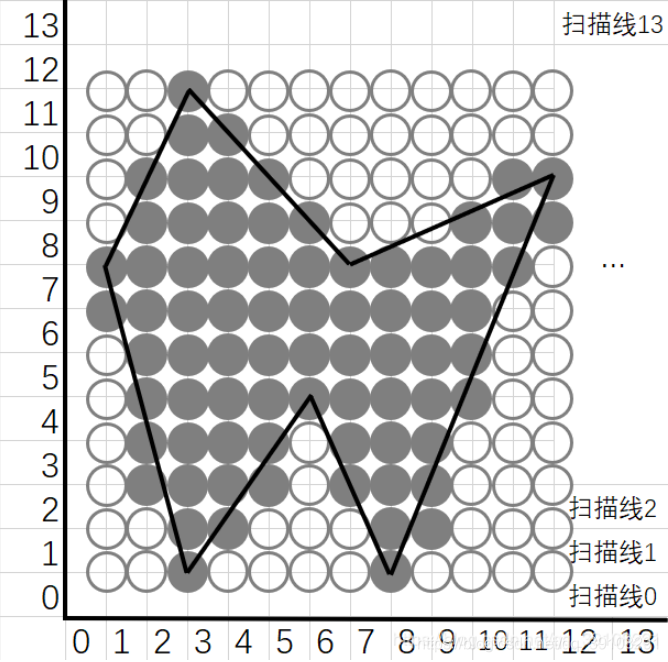

1.2.至此我们发现如下疑问：

​ 1.2.1.像素填充的多边形面积大于多边形实际面积。
​ 可能上图不太明显，我们举一个明显一点的例子，如下正方形：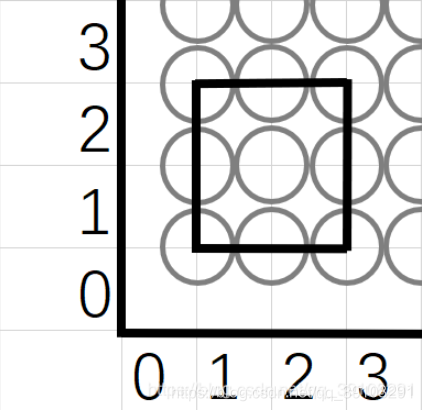

我们填充后的效果为：

​ 而正方形的实际面积是4，在显示器上一个像素为一面积，正方形应该占4个像素点，而实际却占了9个像素点，对于这种问题，有效边表填充算法采用“左闭右开”，“下闭上开”的原则进行像素点的填充，按照此原则，正方形的填充效果如下：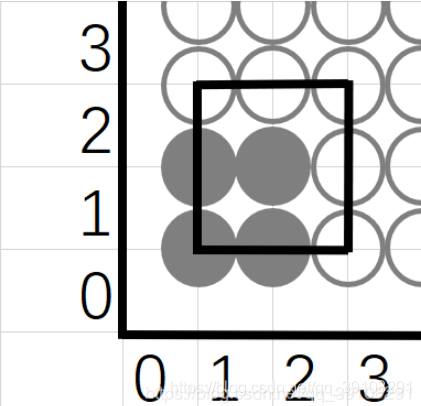

1.2.1.对于点集（1，3）、（1，8）它们分别为扫描线1与P3P2、P3P4、P5P4、P5P6的交点，而在实际计算中它们仍只是两个点，如果处理不当，计算机可能会两两配对得到区间（3，8）而填充到错误的像素区间。
对于此问题，有效边表填充算法采用分类连接点进行处理。
有效边表填充算法将多边形的各个连接点分为三类连接点：

+普通连接点：

​ 连接点所在的两条边分别处于其所在的扫描线的上方和下方，如P2点。

+局部最低点：

​ 连接点所在的两条边都处于其所在的扫描线的上方，如P3、P5点。

+局部最高点：

​ 连接点所在的两条边都处于其所在的扫描线的下方，如：P4、P1、P6点。
​ 在填充开始前，有效边填充算法先对多边形所有的连接点进行分类，判断其在点集中的数量。
有效边填充算法采用如下原则对多边形的连接点进行处理：

1.2.2.普通连接点的处理原则

​ 以P2为例，根据“下闭上开”原则，对于P3P2上的点P2不予填充，P2P1上的点P2需要填充，P2点只填充1次，顾在扫描线7的填充像素点集中P2点的个数记为1，即可以不处理。

1.2.3.局部最低点的处理原则

​ 以P3为例，根据“下闭上开”原则，对于P3P2上的点P3需要填充，P3P4上的点P3也需要填充，P3填充2次，扫描线1的填充像素点集中，再添加一个P3点，使其中有两个P3点，在像素点集中将P3点的个数记为2，P5点进行同样的处理，这样当算法进行两两配对时，得到的像素区间为[3，3]、[5，5]，如此即可避免出现[3，8]的点集区间，解决此类情况的填充错误。

1.2.4.局部最高点的处理原则

​ 以P1点为例，根据“下闭上开”原则，对于P2P1上的P1点不予填充，P0P1上的P1点也不予填充，P1填充0次，扫描线12的像素填充点集中P1点的个数记为0，即从点集中删除P1点，这样的处理符合多边形整体的“下闭上开”原则。
至此，多边形的有效边表填充算法的填充原理已经完成。
但是，我们在填充多边形之前还需要进行一项很重要的工作——根据多边形计算其有效边表，首先我们要了解什么是有效边。
有效边：多边形与当前扫描线相交的边称为有效边，有效边的引入可以有效的避免扫描边与多边形的所有的边进行交点计算，提高算法的效率。
有效边表：有效边按与扫描线交点x坐标递增顺序存放的链表。
有效边表节点结构：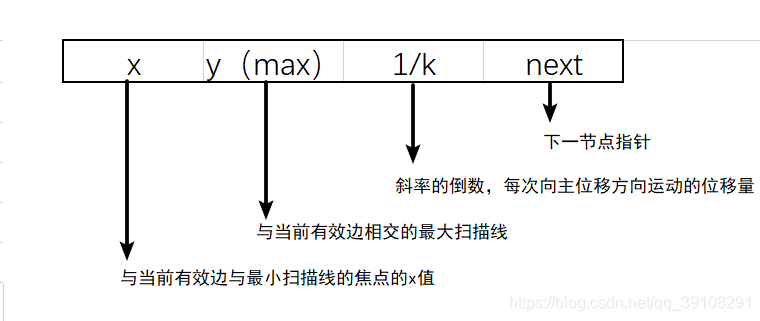

示例：扫描线1的有效边表如下：

桶表：有效边表按扫描线自增顺序存放的表，可以是链表，也可以是顺序表。
桶表的结构：
​ 如：多边形P0-P6的桶表为：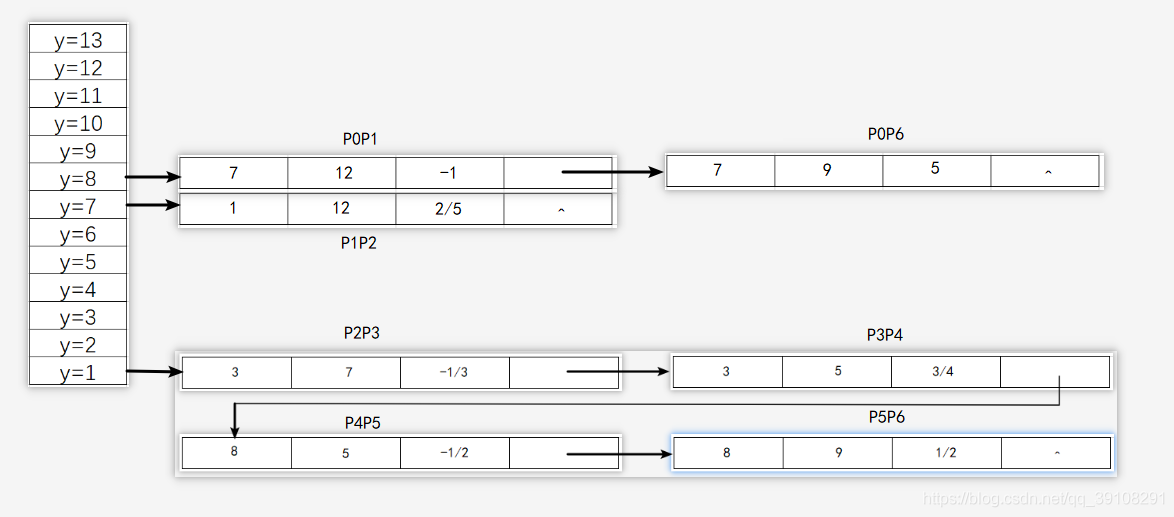

​ 有效边表可以有效的减少计算量，提升多边形的填充效率，如所有的扫描线中，计算机只需要计算扫描线1、扫描线7和扫描线8，且扫描线1只需和边P2P3、P3P4、P4P5、P5P6计算交点，而无需与所有边计算交点，有效边填充算法是目前最有效的多边形填充算法之一。
至此，多边形的有效边填充算法全部完成。

2.边缘填充算法

2.1.算法原理：

​ 先计算多边形每条边与扫描线的交点，然后将交点右侧的所有像素颜色全部取补色。

2.2.补色的定义：

​ 对于黑白图像，白色的补色为黑色，黑色补色为白色，对于彩色图像，前景色取补就是将前景色置为背景色，背景色取补就是将背景声置为前景色。
示例：

​ 边缘填充算法的填充效率受到右侧填充像素的数量影响，当多边形靠近屏幕左侧时，计算机将填充大量无用像素，大大降低的算法的性能，浪费了系统资源。
于是有人提出这样的改进：首先在进行多边形填充之前，先扫描一遍多边形，得出多边形的包围盒，并在适当的位置加入一条栅栏。
包围盒：包围多边形的最小矩形。

2.3.加入包围盒和栅栏的边缘填充算法原理：

​ 每次填充前先判断当前边在栅栏的左侧还是右侧，若在左侧，则取补边以右，栅栏以左的像素；若在右侧，则取补边以右，栅栏以左的像素。
示例：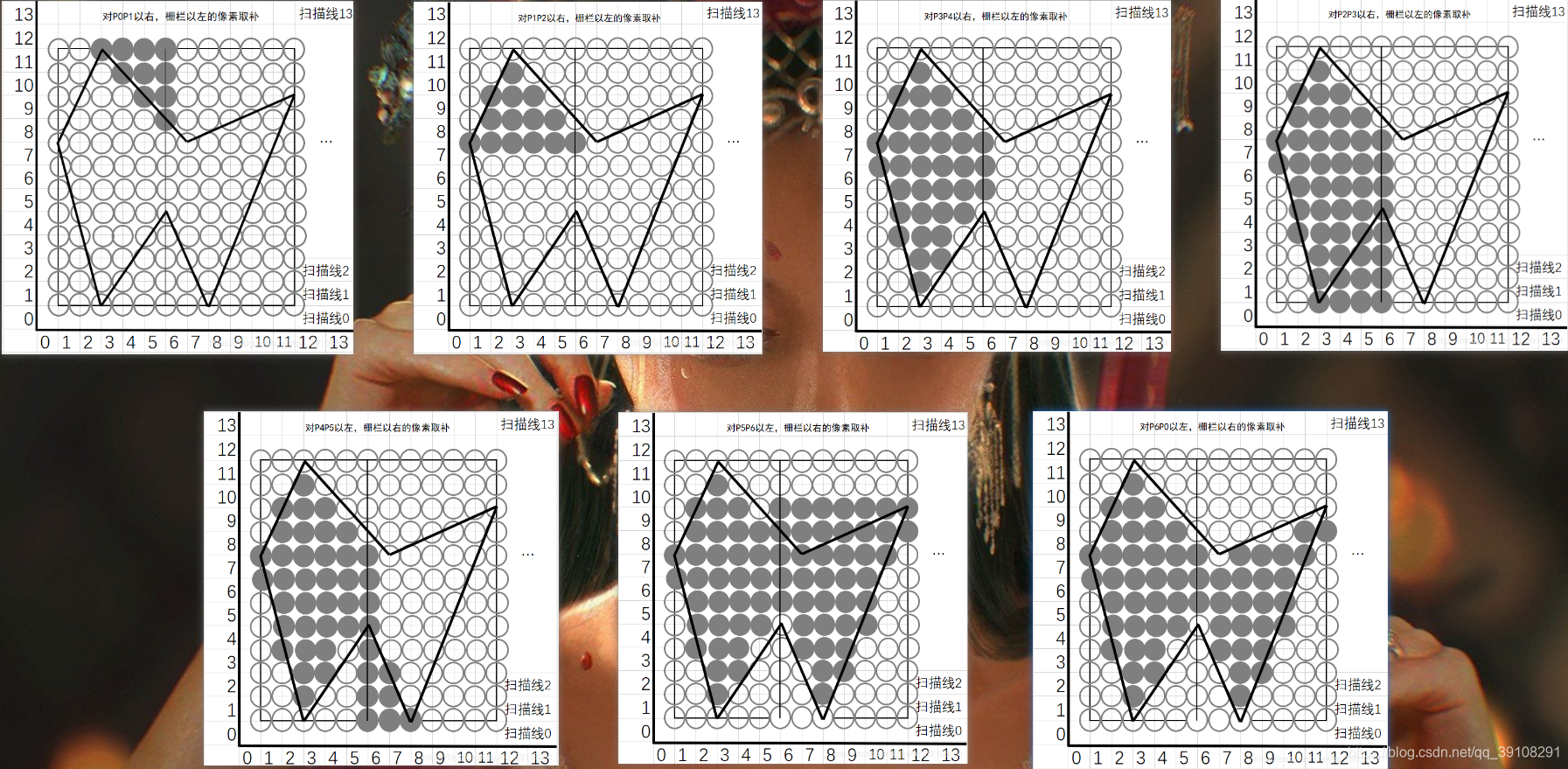

​ 可以看出，加入包围盒和栅栏的边缘填充算法极大的减少了需要填充像素的数量，对填充效率的提升是显著的。
​ 观察边缘填充算法的两幅图，我们是可以察觉到的，边缘填充算法，对多边形的顶点与边的填充不甚理想，边缘填充算法没有给定具体填充时，直线上的点是否包含在填充范围内，笔者试过两种情况的对比——填充时包含直线上的点和填充时不包含直线上的点，得出的结果，多边形的顶点与边的填充都不理想，但是，填充时包含直线上的点的填充方法的最总结果，使多边形在整体上满足“左闭右开”，“下闭上开”原则，顾才用此方法作图。然而，边缘填充算法的填充原理是没有考虑边界的，即多边形的所有像素都填充为一个颜色，无论多边形内部还是多边形的边和顶点，在实际填充效果中，多边形所有像素都填充为一个颜色的填充方式，顶点和边对整体的效果不大，即可以忽略，所以边缘填充算法依旧是效率极高的填充算法之一。

3.种子填充算法

3.1.种子填充算法是区域填充算法中的一种，种子填充算法分为：四邻接点种子填充算法和八邻接点种子填充算法。
在此之前，我们需要了解一些概念：

3.1.1.四邻接点：

​ 任易一个种子像素，其左右上下这四个像素成为这个种子像素的四邻接点。

3.1.2.八邻接点：

​ 任易一个种子像素，其左右上下及左上、右下、右上、左上这八个像素成为这个种子像素的八邻接点。

3.1.3.四连通域：

​ 多边形中能被四邻接点遍历填充的区域。

3.1.4.八连通域：

​ 多边形中能被八邻接点遍历填充的区域。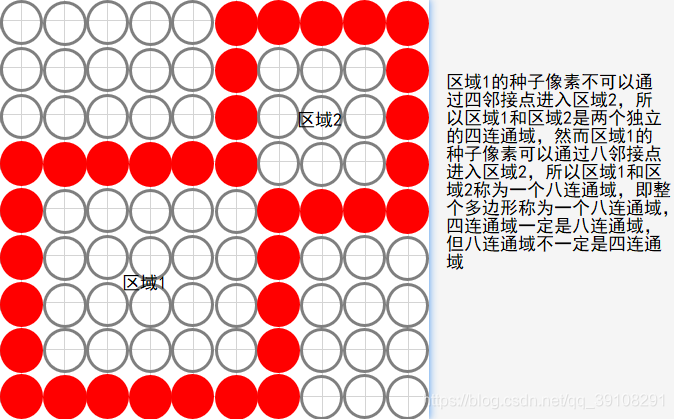

3.1.5.四连通边界：

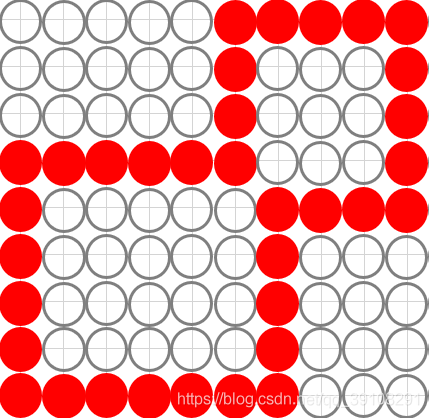
3.1.6.八连通边界：

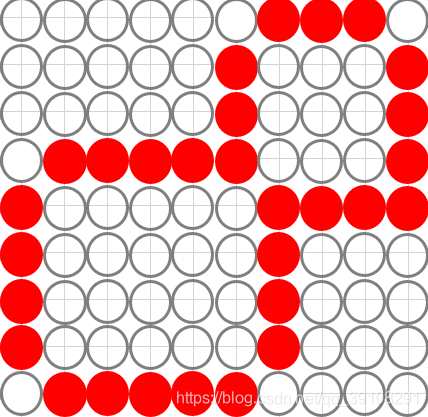
3.2.适用场景：

​ 区域填充算法适用于多边形的边界与内部使用不同的填充色的场景。

3.3.多边形边界的颜色：

​ 边界的颜色由绘制多边形时的画笔确定。

3.4.多边形内部的颜色填充步骤

​ 3.4.1.在多边形内部任易选择一个像素作为种子像素。
​ 3.4.2.将种子像素入栈。
​ 3.4.3.如果栈不为空，则将栈顶元素出栈。
​ 3.4.4.按填充色绘制出栈像素。
​ 3.4.5.按四邻接点（左、上、右、下）（或八邻接点（左、左上、上、右上、右、右下、下、左下））顺序搜索与出栈像素相邻的4（或8）个像素，若该像素的颜色不是填充色并且也不是边界色，则把该像素入栈，否则丢弃该像素。
​ 不难想象，当多边形的面积极大时，入栈的像素像素将是巨量，有的像素可能即是一个像素的邻接点又是另一个像素的邻接点，以致部分像素入栈多次，此情况下填充过程将大量占用栈存储空间，甚至过量占用空间，致使栈空间不足，导致其他程序无空间可用，如此既不能完成填充，又会造成空间溢出，甚至系统崩溃，所以种子填充算法的缺点极为严重。

3.5.改进——扫描种子填充算法

​ 3.5.1.在多边形内部选择一个像素作为种子像素。
​ 3.5.2.将种子像素入栈。
​ 3.5.3.若栈不为空，则将栈顶元素出栈
​ 3.5.4.沿出栈像素所在扫描线，对出栈像素左右像素依次填充，直至遇到边界像素为止。
​ 3.5.5.记录该区间的范围，将最左端的像素记为Xl，将最右端的像素记为Xr。
​ 3.5.6.检查与当前扫描线相邻的上下两条扫描线中在区间[Xl，Xr]里的有关像素是否全为边界像素或以填充像素，若存在非边界且未填充的像素，则把区间最右端像素取作种子像素入栈。
​ 扫描种子填充像素每次只将区间最右端的像素入栈，极大的减少了入栈像素，不仅减少了栈空间的占用，还有效的提高了填充效率和填充速度。